Aller au contenu principal

Modèle de régression linéaire

Comment créer un modèle ultra-simple qui apprend la relation linéaire (équation) y = 2x - 1 avec scikit-learn ?

https://www.youtube.com/watch?v=E6oriD10N_U

Notions théoriques​

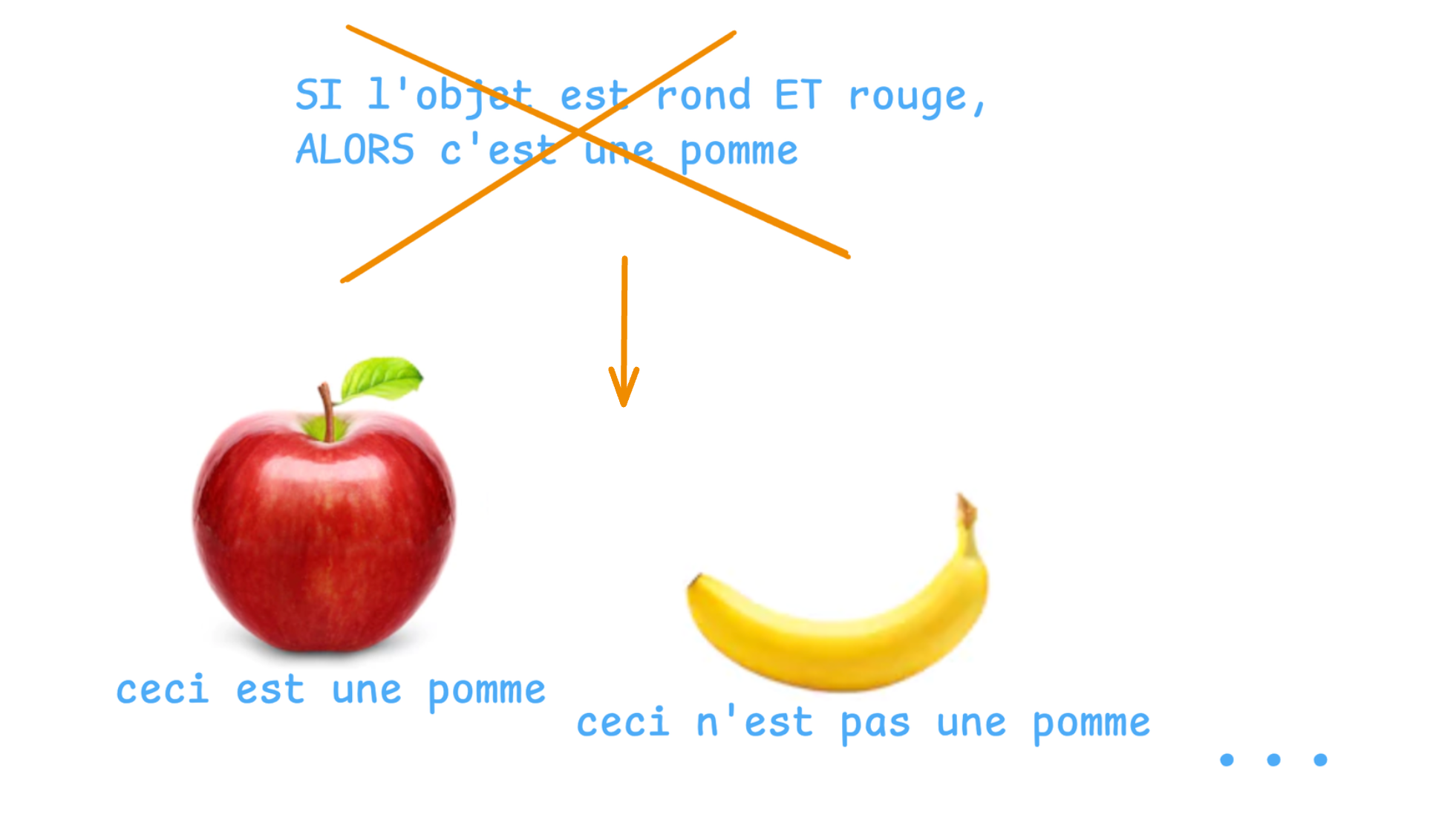
MachineLearning

astuce

Oubliez un instant le code classique et les frameworks de deep learning ;-)

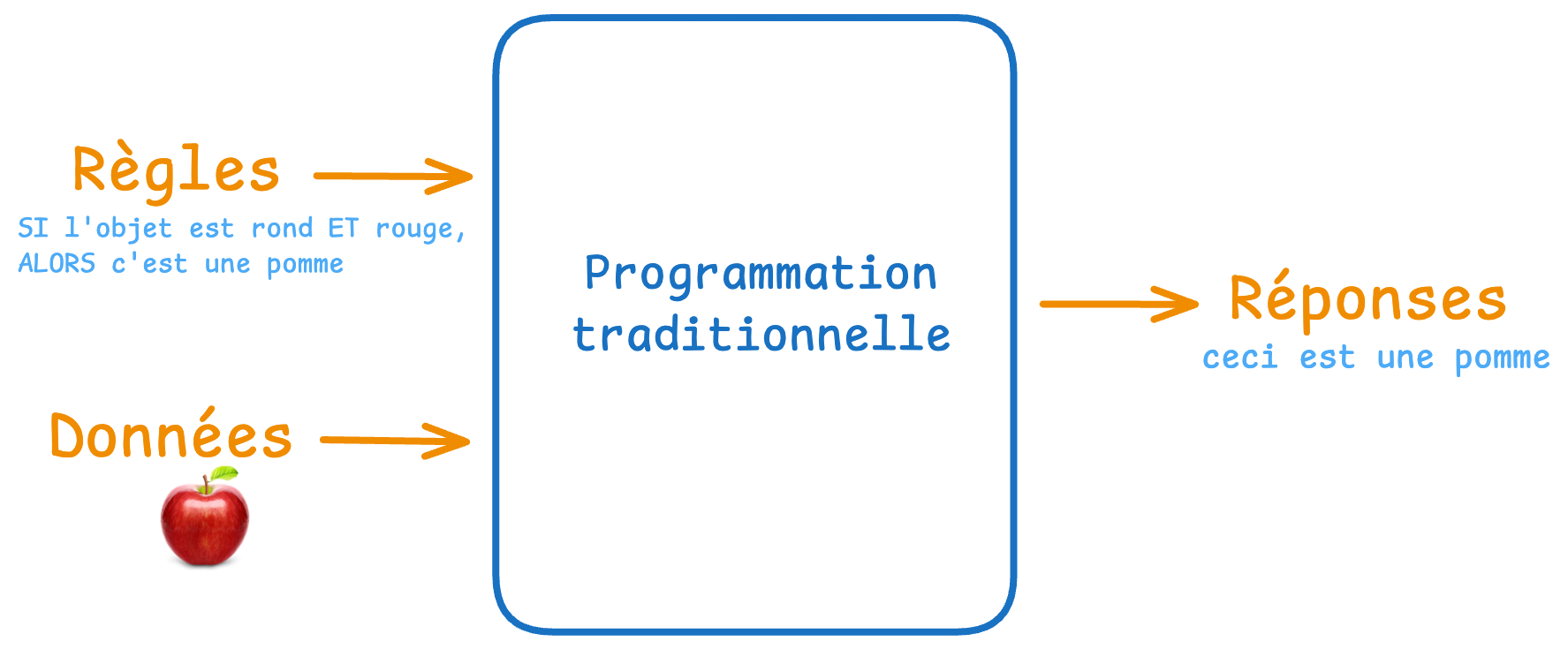
Programmation traditionnelle​

En programmation traditionnelle, vous écrivez des règles strictes : "SI l'objet est rond ET rouge, ALORS c'est une pomme".

1_Programmation traditionnelle

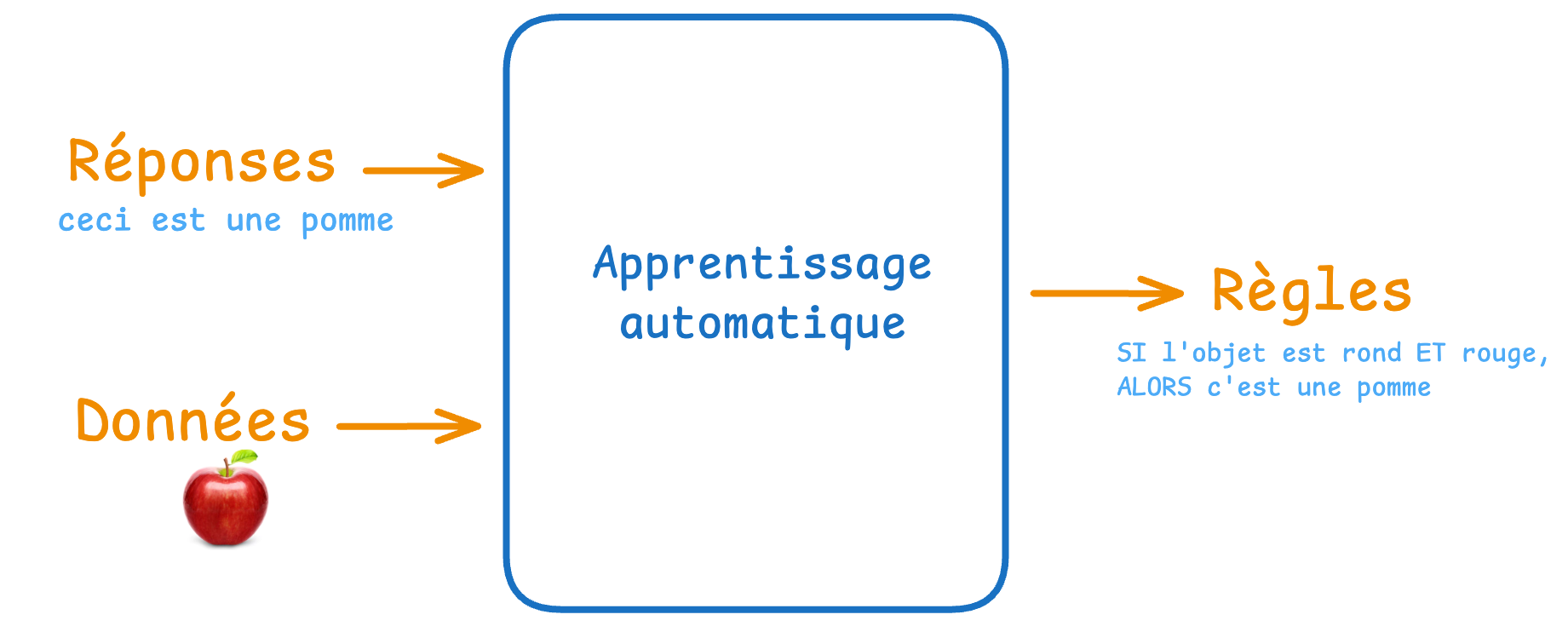
Apprentissage automatique​

L'intelligence artificielle, et plus précisément l'apprentissage automatique (Machine Learning), fonctionne à l'inverse.
Avec l'apprentissage automatique, au lieu de dicter les règles, vous montrez des exemples à la machine, et c'est elle qui trouve elle-même les motifs.

info

C'est la différence entre donner un mode d'emploi et faire un apprentissage par l'observation.

Apprentissage automatique

Exemple pratique​

Voici comment nous allons créer nous-mêmes un modèle d'IA très simple avec scikit-learn.

Commencer par un modèle d'IA facile​

C’est le problème le plus simple possible en apprentissage supervisé.

Avec ce petit modèle, on va aborder toutes les étapes clés de la création d’un modèle de machine learning :

  • la préparation des données
  • la définition du modèle
  • l’entraînement (fit)
  • la prédiction (predict)
  • l’interprétation des paramètres appris (coefficient + intercept)

C’est l’équivalent du « Hello World » en machine learning classique.

Régression linéaire simple​

L'objectif est de créer un modèle qui apprend la relation entre une variable d'entrée x et une variable de sortie y, selon la formule :

  • y = 2x - 1

Exemples :

  • Si x = 3 → y = 5
  • Si x = 7 → y = 13
  • Si x = 10 → y = 19
  • Si x = 8 → y = 15 (valeur jamais vue pendant l'entraînement)
xy attendu (2x - 1)
35
713
1019
-2-5
0-1
1529

Nous allons utiliser scikit-learn, la bibliothèque la plus populaire et la plus pédagogique pour le machine learning classique en Python.

Après entraînement, quand on donnera x = 8 au modèle, il devrait répondre ≈ 15 (exactement ou presque).

La brique élémentaire du Machine Learning
  • La régression linéaire est la brique de base de très nombreux algorithmes.
  • Un réseau de neurones profond n'est finalement qu'un empilement très sophistiqué de régressions linéaires (avec non-linéarités entre elles).

TP pour réfléchir et résoudre des problèmes​

Nous allons créer un programme capable de faire de la régression linéaire simple avec scikit-learn.

Veuillez créer le fichier Python regression_sklearn.py et compléter les étapes ci-dessous.

0. Préparation de l'environnement​

# Créer un environnement virtuel (recommandé)
python3.10 -m venv venv_sklearn
source venv_sklearn/bin/activate     # macOS/Linux
# venv_sklearn\Scripts\activate      # Windows

# Installer les packages
pip install numpy matplotlib scikit-learn

1. Importations Python nécessaires​

import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error

2. Création des données d’entraînement​

Très peu de points suffisent ici.

# Données d'apprentissage
X = np.array([-2.0, 0.0, 3.0, 7.0, 10.0, 15.0]).reshape(-1, 1)  # shape (n_samples, 1)
y = 2 * X.ravel() - 1   # ou bien : y = 2 * X[:,0] - 1

print("X =", X.ravel())
print("y =", y)

Sortie attendue :

X = [-2. 0. 3. 7. 10. 15.]
y = [ -5. -1.  5. 13. 19. 29.]

3. Visualisation rapide des données​

plt.figure(figsize=(7,5))
plt.scatter(X, y, color='darkorange', s=100, label='Données réelles')
plt.xlabel('X')
plt.ylabel('y')
plt.title('Données à apprendre : y = 2X - 1')
plt.grid(True, alpha=0.3)
plt.legend()
plt.show()

4. Définition et entraînement du modèle​

scikit-learn est très direct :

model = LinearRegression()

model.fit(X, y)

→ Pas besoin de compiler, pas d'epochs, pas d'optimizer à choisir manuellement : tout est automatique (moindres carrés ordinaires = Ordinary Least Squares).

5. Regardons les paramètres appris​

print(f"Poids (coefficient) appris : {model.coef_[0]:.4f}")
print(f"Biais (intercept) appris   : {model.intercept_:.4f}")

Résultat typique :

Poids (coefficient) appris : 2.0000
Biais (intercept) appris   : -1.0000

→ Exactement 2 et -1 (ou extrêmement proche) → le modèle a parfaitement compris la relation !

6. Prédictions​

X_test = np.array([1.0, 4.0, 8.0, 20.0]).reshape(-1, 1)
predictions = model.predict(X_test)

for x, pred in zip(X_test.ravel(), predictions):
    print(f"X = {x:3.0f} → prédiction = {pred:6.2f} (attendu : {2*x-1:6.2f})")

Exemple de sortie :

X =   1 → prédiction =  1.00 (attendu :  1.00)
X =   4 → prédiction =  7.00 (attendu :  7.00)
X =   8 → prédiction = 15.00 (attendu : 15.00)
X =  20 → prédiction = 39.00 (attendu : 39.00)

7. Visualisation finale – tout ensemble​

plt.figure(figsize=(8,6))
# Données d'entraînement
plt.scatter(X, y, color='darkorange', s=120, label='Données entraînement')
# Prédictions sur une grille fine
X_grid = np.linspace(-3, 16, 100).reshape(-1, 1)
y_grid = model.predict(X_grid)
plt.plot(X_grid, y_grid, 'b-', linewidth=2.5, label='Modèle appris')
plt.xlabel('X')
plt.ylabel('y')
plt.title('Régression linéaire – y ≈ 2X - 1 (scikit-learn)')
plt.grid(True, alpha=0.3)
plt.legend()
plt.show()

Corrigé​

📌 Une solution possible

Test de mémorisation/compréhension​

  1. Combien de paramètres le modèle a-t-il appris ?
  2. Pourquoi scikit-learn trouve-t-il la solution exacte ici alors que TensorFlow avait une toute petite erreur ?
  3. À quoi correspond model.coef_ dans ce cas ?
  4. Quelle est la différence principale entre model.fit() ici et model.fit(..., epochs=500) avec Keras ?
  5. Pourquoi la prédiction sur X=8 est-elle exactement 15 même si 8 n’était pas dans les données d’entraînement ?