Aller au contenu principal

Une adresse IP en binaire

Rappels​

Qu'est-ce qu'une adresse IP ?​

Une adresse IP (Internet Protocol) est un numéro unique attribué à chaque appareil connecté à un réseau informatique utilisant le protocole IP.

Une adresse IP permet d'identifier de manière unique chaque appareil sur le réseau.

Les versions d'adresses IP​

Il existe 2 versions d'adresses IP :

  • IPv4 : Elle utilise des adresses de 32 bits, généralement représentées sous forme de quatre nombres décimaux séparés par des points (par exemple, 192.168.1.1).
  • IPv6 : Elle utilise des adresses de 128 bits, représentées sous forme de huit groupes de quatre chiffres hexadécimaux séparés par des deux-points (par exemple, 2001:0db8:85a3:0000:0000:8a2e:0370:7334).

Comment convertir un nombre en binaire ?​

Important

C'est l'heure de jouer aux détectives des chiffres !

Sortez une feuille et un crayon, et mettons-nous à la conversion binaire.

Avec un peu de chance, vous découvrirez que les maths peuvent être aussi amusantes qu'un bon jeu vidéo !

Méthode pour convertir un nombre en binaire de 8 bits​

Voici une méthode simple basée sur la soustraction des puissances de 2.

Il suffit de suivre ces 4 étapes :

  1. Choisissez le nombre à convertir

    • Par exemple, prenons le nombre 172.

  2. Écrivez la suite des puissances de 2 à utiliser

    • Ordre des comparaisons : 128, 64, 32, 16, 8, 4, 2, 1

  3. Comparez avec chaque puissance de 2

    • Pour chaque puissance de 2 dans l'ordre décroissant :
      • Si le nombre est supérieur ou égal à la puissance de 2, notez un 1 et soustrayez cette puissance du nombre.
      • Si le nombre est inférieur, notez un 0.

  4. Écrivez le résultat final

    • Le binaire obtenu sera la séquence de 1 et de 0 que vous avez notée, correspondant aux puissances de 2.

Exemple avec le nombre 172 :​

  1. Nombre à convertir : 172

  2. Suite des puissances de 2 : 128, 64, 32, 16, 8, 4, 2, 1

  3. Comparaisons :

    • 172 ≥ 128 : 1 (172 - 128 = 44)
    • 44 < 64 : 0
    • 44 ≥ 32 : 1 (44 - 32 = 12)
    • 12 < 16 : 0
    • 12 ≥ 8 : 1 (12 - 8 = 4)
    • 4 ≥ 4 : 1 (4 - 4 = 0)
    • 0 < 2 : 0
    • 0 < 1 : 0

  4. Résultat final : 172 en binaire = 10101100

Méthode n°2

Voici une autre méthode, pour convertir un nombre en binaire de 8 bits, que certaines personnes préfèrent.

Il suffit de suivre ces 4 étapes :

  1. Choisir le nombre à convertir

    • Par exemple, prenons le nombre 172.

  2. Diviser le nombre par 2 et noter le reste

    • Diviser le nombre par 2 et noter le quotient et le reste. Le reste sera soit 0 soit 1.
    • Répéter ce processus avec le quotient obtenu jusqu'à ce que le quotient soit 0.

  3. Écrire les restes en ordre inverse

    • Les restes obtenus à chaque étape formeront le nombre binaire. Écrivez-les en partant du dernier reste obtenu jusqu'au premier.

  4. Compléter avec des zéros pour obtenir 8 bits

    • Si le nombre binaire obtenu a moins de 8 bits, ajouter des zéros à gauche pour compléter jusqu'à 8 bits.

Exemple : Convertir le nombre 172 en binaire de 8 bits​

  1. Choisir le nombre :

    • nombre = 172

  2. Diviser par 2 et noter les restes :

    Division par 2QuotientReste
    172 ÷ 2860
    86 ÷ 2430
    43 ÷ 2211
    21 ÷ 2101
    10 ÷ 250
    5 ÷ 221
    2 ÷ 210
    1 ÷ 201

  3. Écrire les restes en ordre inverse :

    • En partant du dernier reste obtenu jusqu'au premier : 10101100

  4. Compléter avec des zéros pour obtenir 8 bits :

    • Ici, le nombre binaire obtenu est déjà de 8 bits : 10101100
Résultat​

Le nombre 172 converti en binaire de 8 bits est : 10101100

Résumé des étapes de cette 2ème méthode​

  1. Diviser le nombre par 2.
  2. Noter le reste (0 ou 1).
  3. Répéter avec le quotient jusqu'à obtenir 0.
  4. Écrire les restes en ordre inverse.
  5. Compléter avec des zéros à gauche pour obtenir 8 bits si nécessaire.

astuce

En suivant l'une de ces méthodes, vous pouvez facilement convertir n'importe quel nombre en binaire de 8 bits.

A vous de jouer ! Convertissez le nombre 16 en binaire de 8 bits.​

  1. Choisissez le nombre à convertir

  2. Écrivez la suite des puissances de 2 à utiliser

    • Ordre des comparaisons : 128, 64, 32, 16, 8, 4, 2, 1

  3. Comparez avec chaque puissance de 2

    • Pour chaque puissance de 2 dans l'ordre décroissant :
      • Si le nombre est supérieur ou égal à la puissance de 2, notez un 1 et soustrayez cette puissance du nombre.
      • Si le nombre est inférieur, notez un 0.

  4. Écrivez le résultat final

    • Le binaire obtenu sera la séquence de 1 et de 0 que vous avez notée, correspondant aux puissances de 2.
Solution
Solution avec la méthode n°2

A vous de jouer ! Convertissez le nombre 168 en binaire de 8 bits.​

  1. Choisissez le nombre à convertir

  2. Écrivez la suite des puissances de 2 à utiliser

    • Ordre des comparaisons : 128, 64, 32, 16, 8, 4, 2, 1

  3. Comparez avec chaque puissance de 2

    • Pour chaque puissance de 2 dans l'ordre décroissant :
      • Si le nombre est supérieur ou égal à la puissance de 2, notez un 1 et soustrayez cette puissance du nombre.
      • Si le nombre est inférieur, notez un 0.

  4. Écrivez le résultat final

    • Le binaire obtenu sera la séquence de 1 et de 0 que vous avez notée, correspondant aux puissances de 2.
Solution
Solution avec la méthode n°2

A vous de jouer ! Convertissez le nombre 192 en binaire de 8 bits.​

  1. Choisissez le nombre à convertir

  2. Écrivez la suite des puissances de 2 à utiliser

    • Ordre des comparaisons : 128, 64, 32, 16, 8, 4, 2, 1

  3. Comparez avec chaque puissance de 2

    • Pour chaque puissance de 2 dans l'ordre décroissant :
      • Si le nombre est supérieur ou égal à la puissance de 2, notez un 1 et soustrayez cette puissance du nombre.
      • Si le nombre est inférieur, notez un 0.

  4. Écrivez le résultat final

    • Le binaire obtenu sera la séquence de 1 et de 0 que vous avez notée, correspondant aux puissances de 2.
Solution
Solution avec la méthode n°2

A vous de jouer ! Convertissez le nombre 254 en binaire de 8 bits.​

  1. Choisissez le nombre à convertir

  2. Écrivez la suite des puissances de 2 à utiliser

    • Ordre des comparaisons : 128, 64, 32, 16, 8, 4, 2, 1

  3. Comparez avec chaque puissance de 2

    • Pour chaque puissance de 2 dans l'ordre décroissant :
      • Si le nombre est supérieur ou égal à la puissance de 2, notez un 1 et soustrayez cette puissance du nombre.
      • Si le nombre est inférieur, notez un 0.

  4. Écrivez le résultat final

    • Le binaire obtenu sera la séquence de 1 et de 0 que vous avez notée, correspondant aux puissances de 2.
Solution
Solution avec la méthode n°2

A vous de jouer ! Convertissez le nombre 240 en binaire de 8 bits.​

  1. Choisissez le nombre à convertir

  2. Écrivez la suite des puissances de 2 à utiliser

    • Ordre des comparaisons : 128, 64, 32, 16, 8, 4, 2, 1

  3. Comparez avec chaque puissance de 2

    • Pour chaque puissance de 2 dans l'ordre décroissant :
      • Si le nombre est supérieur ou égal à la puissance de 2, notez un 1 et soustrayez cette puissance du nombre.
      • Si le nombre est inférieur, notez un 0.

  4. Écrivez le résultat final

    • Le binaire obtenu sera la séquence de 1 et de 0 que vous avez notée, correspondant aux puissances de 2.
Solution
Solution avec la méthode n°2

Conversion d'une adresse IPv4 en binaire​

Méthode​

Pour convertir une adresse IPv4 en binaire, vous devez convertir chaque octet (chaque nombre entre les points) en son équivalent binaire de 8 bits, puis regrouper les résultats.

Il suffit de suivre ces 2 étapes :

  1. convertir chaque octet en binaire

  2. regrouper les résultats

Exemples pratiques​

Prenons 2 exemples pratiques pour bien comprendre la conversion d'une adresse IPv4.

Exemple 1 : Conversion de l'adresse IP 192.168.1.1​

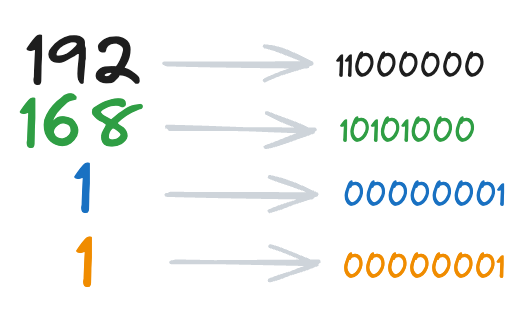
  1. Convertir chaque octet en binaire :

    • 192 en binaire : 11000000
    • 168 en binaire : 10101000
    • 1 en binaire : 00000001
    • 1 en binaire : 00000001

  2. Regrouper les résultats :

    • 192.168.1.1 en binaire est : 11000000.10101000.00000001.00000001

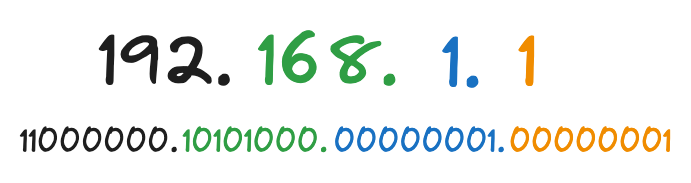
Exemple 2 : Conversion de l'adresse IP 172.16.254.1​

  1. Convertir chaque octet en binaire :

    • 172 en binaire : 10101100
    • 16 en binaire : 00010000
    • 254 en binaire : 11111110
    • 1 en binaire : 00000001

  2. Regrouper les résultats :

    • 172.16.254.1 en binaire est : 10101100.00010000.11111110.00000001

Test de mémorisation/compréhension​


Quelle est l'adresse IP 192.168.0.1 en binaire ?


Quel est le format de l'adresse IPv4 ?


Quel est le format de l'adresse IPv6 ?


L'adresse IP 10.0.0.1 est-elle une adresse publique ou privée ?


TP pour réfléchir et résoudre des problèmes​

Le but de ce TP est de vous faire pratiquer la conversion d'adresses IP pour bien mémoriser la méthode de calcul.

Convertissez les adresses IP suivantes en binaire :

  • 10.0.0.1

    Solution
    Solution avec la méthode n°2

  • 172.16.0.1

    Solution

  • 192.168.100.1

    Solution

Entrainement​

La conversion en binaire permet de mieux comprendre la structure des adresses IP et facilite les calculs de sous-réseaux.

Voici une liste de 10 adresses IPv4 intéressantes à convertir en binaire, car elles représentent différents types d'adresses couramment utilisées dans les réseaux.

  1. 224.0.0.1

    Solution

  2. 169.254.0.1

    Solution

  3. 192.0.2.1

    Solution

  4. 198.51.100.1

    Solution

  5. 192.168.0.1 (adresse IP privée courante)

    Solution

  6. 127.0.0.1 (adresse localhost)

    Solution

  7. 8.8.8.8 (DNS public de Google)

    Solution

  8. 255.255.255.255 (adresse de diffusion)

    Solution

  9. 10.0.0.1 (première adresse du réseau privé de classe A)

    Solution

  10. 172.16.0.1 (première adresse du réseau privé de classe B)

Solution